
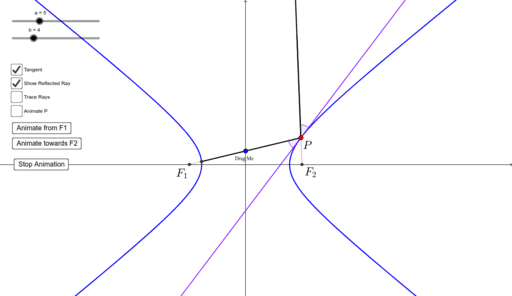
I think if I spend another week on it I'd probably narrow down something that worked, but I'm sure this is a common, easy problem to solve, and would really appreciate any links or whatever help you can give. For the ellipse, a beam emanating from a focus is reflected by the curve through. Which works for about 1/8th of use cases. var x = h / xRadius var y = k / yRadius xMomentum *= xM * (x - y) + yM * (x / y) yMomentum *= yM * (y - x) + xM * (y / x) x and y are distance from h and k or sin / cos of the angle from center.
I'm getting closer to the reflection equation every day, but just can't find the answer online anywhere. Object is always at (0, 0) so I don't need to subtract x and y from h and k const d = h^2 / xRadius^2 + k^2 / yRadius^2 if (d <= 1) I'm now at the point where I have bounded ellipses that move the player out using:
to see the current version that has the old bounding boxes. Get access to the latest L17: Illustrations based on reflection property on Ellipse and Hyperbola (in Hindi) prepared with IIT JEE course curated by. I finally decided to tackle a more realistic feeling elliptical bounding method.
#ANGLE OF REFLECTION ELLIPSE SERIES#
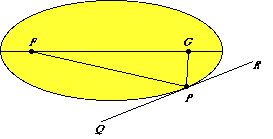
Hi, I've been programming my first game for a while now, and finally decided that a series of small bounding boxes around the inside of an ellipse just wasn't cutting it anymore. I guess I will just have to wait and see.TLDR: What is the equation for reflection off of the surface of an ellipse? We aren't even close to knowing all the things we need to know about the conic sections. I am really curious to see if the equations are harder to solve then the 2d equations. Which I figured out while doing this project because I learned there was a 3d case to all of these, which it blew my mind. I feel like we learned a lot of stuff this unit, but I bet that was just the basic and there is much more to come. In view of the symmetry about the X axis and Y axis, the angle between the ellipse and circle is the same for all the points of intersection and hence we. Then, there is the circle, which is unique, its center point is both of the foci. A good example of this would be a cd because it clearly shows the center point. Last but not least, there is the hyberbola, which is a smoke stack structure that sends the rays outward instead of inward. For example, the stars in the sky when you stand in one place and see something but someone standing 20 miles away cannot see it. For the ellipse though it is about the same properties except it is from one focus to the other focus instead of wall to focus. I think it is pretty cool how in in a parabola, if the ray approaches the curved line it will reflect to the focus from any point or angle inside of the parabola's "mouth." For example, a satelite, how it sends and receives signals. Since the copy is a faithful reproduction of the actual journal pages, the article may not begin at the top of the.
#ANGLE OF REFLECTION ELLIPSE PDF#
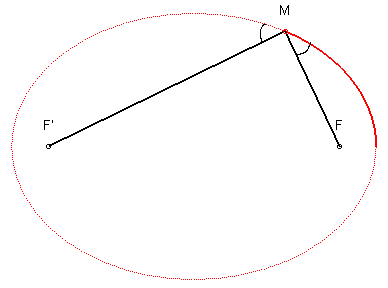
A pdf copy of the article can be viewed by clicking below. tan m 1 m 2 1 + m 1 m 2 tan m 1 m 3 1 + m 1 m 3 tan tan. A polar coordinate proof of the fact that the focal radii of an elipse (hyperbola) make equal angles with the tangent. Since the line segment P R (slope m 2) is equally inclined to the tangent ( slope m 1) as the segment Q R ( slope m 3 ), we can equalise the angles. Throughout this unit, I learned a lot about the conic sections. Applicable Course (s): 3.1 Mainstream Calculus I.


 0 kommentar(er)
0 kommentar(er)
